Binary search - tìm kiếm nhị phân

1. Giới thiệu

Thuật toán Tìm kiếm nhị phân (Binary Search) là một thuật toán cao cấp tìm kiếm tuyến tính hơn với thời gian chạy là O(logN). Đối với các danh sách lớn, thuật toán này tốt hơn hẳn tìm kiếm tuyến tính, nhưng nó đòi hỏi danh sách phải được sắp xếp từ trước (xem phân loại thuật toán sắp xếp) và đòi hỏi khả năng truy nhập ngẫu nhiên (random access).

Thuật toán tìm kiếm nhị phân dùng để tìm kiếm phần tử trong một danh sách đã được sắp xếp, ví dụ như trong một danh bạ điện thoại sắp xếp theo tên, có thể tìm kiếm số điện thoại của một người theo tên người đó.

Thuật toán tìm kiếm nhị phân chạy nhanh hơn tìm kiếm tuần tự nhưng cũng có một số nhược điểm. Tìm kiếm nhị phân có thể chậm hơn bảng băm. Nếu nội dung danh sách bị thay đổi thì danh sách phải được sắp xếp lại trước khi sử dụng tìm kiếm nhị phân. Thao tác này thường tốn nhiều thời gian.

2. Ý tưởng và minh hoạ

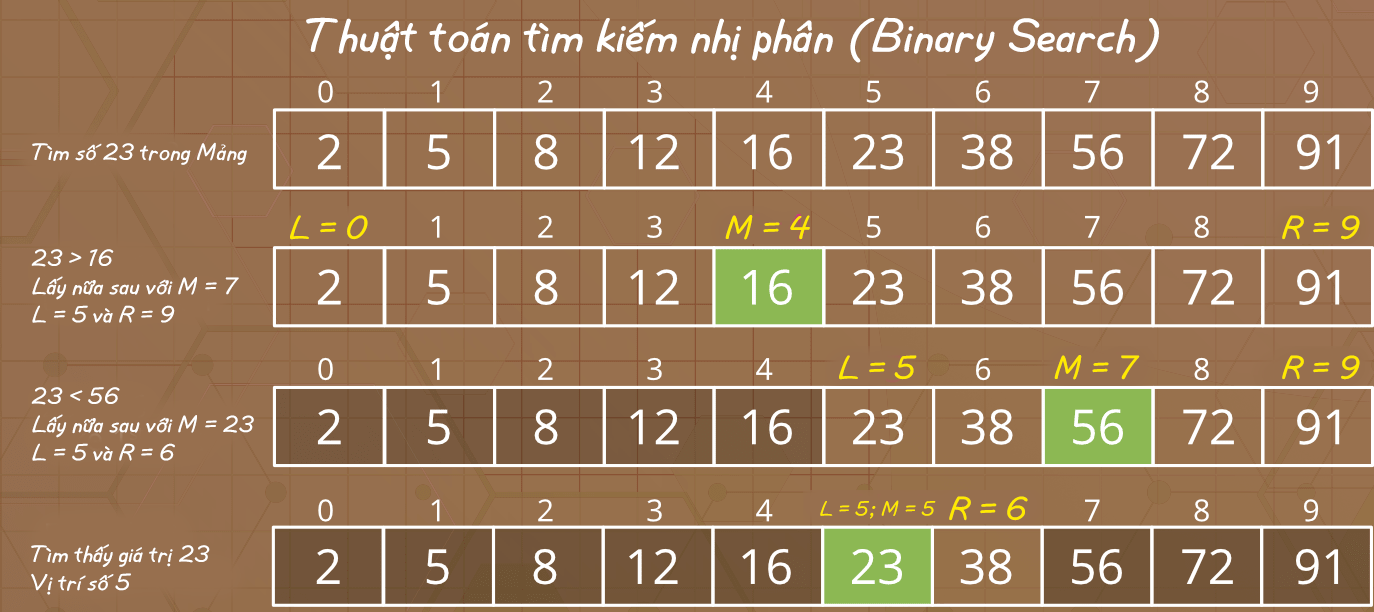
Tìm kiếm nhị phân so sánh giá trị đích với phần tử ở giữa của mảng.

Nếu chúng không bằng nhau, một nửa trong đó không chứa mục tiêu tìm kiếm bị loại bỏ và việc tìm kiếm tiếp tục ở nửa còn lại, một lần nữa lấy phần tử ở giữa được chọn để so sánh với giá trị đích và lặp lại điều này cho đến khi tìm thấy giá trị đích.

Nếu tìm kiếm kết thúc với nửa còn lại trống, mục tiêu không nằm trong mảng. Mặc dù ý tưởng rất đơn giản, nhưng việc thực hiện tìm kiếm nhị phân chính xác đòi hỏi phải chú ý đến một số điểm tinh tế về điều kiện thoát và tính toán điểm giữa của nó.

Minh họa Thuật toán tìm kiếm nhị phân ví dụ minh họa ở hình trên, Tìm vị trí phần tử có giá trị là 72 trong một mảng A[2, 5, 8, 12, 16, 23, 38, 56, 72, 91] đã được sắp xếp. Về cơ bản bạn loại bỏ được một nửa các yếu tố chỉ sau một lần so sánh.

• So sánh x với phần tử ở giữa.
• Nếu x khớp với phần tử ở giữa, chúng ta trả về chỉ số giữa.
• Khác Nếu x lớn hơn phần tử mid, thì x chỉ có thể nằm trong nửa phân đoạn bên phải sau phần tử mid. Vì vậy, chúng ta chỉ tìm kiếm ở nữa phải của mảng.
• Khác (x nhỏ hơn) tiếp tục cho nửa bên trái.
• Lặp lại đến khi tìm ra x hoặc trả về null khi x không nằm trong mảng.

3. Code demo

Từ ví dụ minh hoạ trên hình ở mục 2, chúng ta hãy triển khai nó sang code xem như thế nào.

public class BinarySearch {

    // Trả về chỉ mục của x nếu nó có trong arr[l..r]
    // ngược lại trả về -1
    int binarySearch(int arr[], int l, int r, int x) {
        if (r >= l) {
            int mid = l + (r - l) / 2;

            // Nếu phần tử có ở chính giữa
            if (arr[mid] == x)
                return mid;

            // Nếu phần tử nhỏ hơn giữa, thì nó chỉ có thể
            // hiện diện trong mảng con bên trái
            if (arr[mid] > x)
                return binarySearch(arr, l, mid - 1, x);

            // Ngược lại, phần tử chỉ có thể có mặt
            // trong mảng con bên phải
            return binarySearch(arr, mid + 1, r, x);
        }

        // Nếu phầnt tử không có trong mảng
        return -1;
    }

    public static void main(String args[]) {
        BinarySearch ob = new BinarySearch();
        int arr[] = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91};
        int n = arr.length;
        int x = 72;
        int result = ob.binarySearch(arr, 0, n - 1, x);
        if (result == -1)
            System.out.println("Phần tử không tồn tại.");
        else
            System.out.println("Phần tử được tìm thấy tại: " + result);
    }
}

Tuy nhiên BinarySearch cũng có thể viết theo một cách khác, tương tự như trên nhưng chúng ta sẽ lặp đi lặp lại phần tử.

package binary.search.algo;

public class IterativeBinarySearch {

    // Trả về chỉ mục của x nếu nó có trong arr[l..r]
    // ngược lại trả về -1
    int binarySearch(int arr[], int x) {
        int l = 0, r = arr.length - 1;
        while (l <= r) {
            int m = l + (r - l) / 2;

            // kiểm tra xem x có ở chính giữa không
            if (arr[m] == x)
                return m;

            // Nếu x lớn hơn, bỏ qua nửa bên trái
            if (arr[m] < x)
                l = m + 1;

                // Nếu x nhỏ hơn, bỏ qua nửa bên phải
            else
                r = m - 1;
        }

        // phần tử không tồn tại
        return -1;
    }

    public static void main(String args[]) {
        BinarySearch ob = new BinarySearch();
        int arr[] = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91};
        int n = arr.length;
        int x = 72;
        int result = ob.binarySearch(arr, x);
        if (result == -1)
            System.out.println("Phần tử không tồn tại.");
        else
            System.out.println("Phần tử được tìm thấy tại: " + result);
    }
}

Binary Search có lợi thế lớn về độ phức tạp thời gian khi so sánh với các thuật toán tìm kiếm khác. Điều đặc biệt đối với tìm kiếm nhị phần là mảng cần phải được sắp xếp trước đó, nên việc bạn áp dụng một thuật toán sắp xếp nào đó mà mình đã chia sẻ hôm trước là một điều gần như là bắt buộc.

Binary Search là thuật toán quan trọng và được ứng dụng nhiều trong cuộc sống. Việc các thuật toán kết hợp và bổ trợ cho nhau là điều không thể tránh khỏi, và việc bạn cần phải biết càng nhiều thuật toán thông dụng cũng là việc khó tránh khỏi.

Bài viết mang tính chất “ghi chú, lưu trữ, chia sẻ và phi lợi nhuận”.
Nếu bạn thấy hữu ích, đừng quên chia sẻ với bạn bè và đồng nghiệp của mình nhé!

Happy coding! 😎 👍🏻 🚀 🔥