Merge sort - sắp xếp trộn

1. Giới thiệu

Trong khoa học máy tính, sắp xếp trộn (Merge Sort) là một thuật toán sắp xếp để sắp xếp các danh sách (hoặc bất kỳ cấu trúc dữ liệu nào có thể truy cập tuần tự) theo một trật tự nào đó. Nó được xếp vào thể loại sắp xếp so sánh. Thuật toán này là một ví dụ tương đối điển hình của lối thuật toán chia để trị do John von Neumann đưa ra lần đầu năm 1945.

Thuật toán sắp xếp Merge Sort là một trong những thuật toán có độ phức tạp ở mức trung bình và cùng sử dùng phương pháp chia để trị giống thuật toán sắp xếp nhanh Quick Sort. Thuật toán này không chỉ áp dụng trong sắp xếp mà còn ở nhiều bài toán khác.

Ý tưởng của giải thuật này bắt nguồn từ việc trộn 2 danh sách đã sắp xếp thành 1 danh sách mới cũng được sắp xếp.

Giả sử có hai danh sách đã được sắp xếp a[1..m] và b[1..n]. Ta có thể trộn chúng lại thành một danh sách mới c[1..m+n] được sắp xếp theo cách sau:

• So sánh hai phần tử đứng đầu của hai danh sách, lấy phần tử nhỏ hơn cho vào danh sách mới. Tiếp tục như vậy cho tới khi một trong hai danh sách là rỗng.
• Khi một trong hai danh sách là rỗng ta lấy phần còn lại của danh sách kia cho vào cuối danh sách mới. Độ phức tạp thuật toán: O(nlog(n))

2. Ý tưởng và mô tả triển khai

Ý tưởng để áp dụng cho một Merge Sort được mô tả ngắn gọn như trong code giả bên dưới:

mergeSort(arr[], l, r)
if r > l
1. Tìm chỉ số nằm giữa mảng để chia mảng thành 2 nửa:
middle m = (l+r)/2
2. Gọi đệ quy hàm mergeSort cho nửa đầu tiên:
mergeSort(arr, l, m)
3. Gọi đệ quy hàm mergeSort cho nửa thứ hai:
mergeSort(arr, m+1, r)
4. Gộp 2 nửa mảng đã sắp xếp ở (2) và (3):
merge(arr, l, m, r)

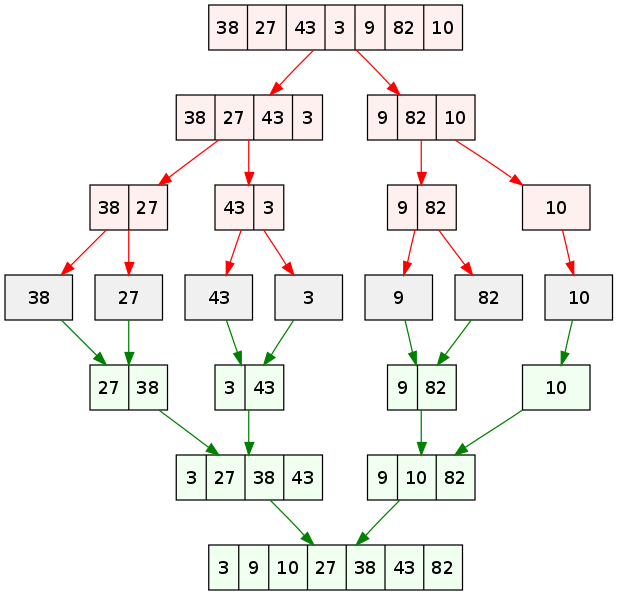
Hình ảnh trên hiển thị cho bạn toàn bộ sơ đồ tiến trình của thuật toán merge sort cho mảng {38, 27, 43, 3, 9, 82, 10}.

Nếu nhìn kỹ hơn vào sơ đồ này, chúng ta có thể thấy mảng ban đầu được lặp lại hành động chia cho tới khi kích thước các mảng sau chia là 1. Khi kích thước các mảng con là 1, tiến trình gộp sẽ bắt đầu thực hiện gộp lại các mảng này cho tới khi hoàn thành và chỉ còn một mảng đã sắp xếp.

3. Code demo

Như các bài chia sẻ trước, chung ta hãy triển khai ý tưởng của mục 2 thành code xem như thế nào?

public class MergeSort {

    // Merge hai mảng con của arr[].
    // Mảng con thứ nhất là arr[l..m]
    // Mảng con thứ hai là arr[m+1..r]
    void merge(int arr[], int l, int m, int r) {

        // Tìm kích thước của 2 mảng con để merged
        int n1 = m - l + 1;
        int n2 = r - m;

        // Tạo mảng tạm
        int L[] = new int[n1];
        int R[] = new int[n2];

        // Copy dữ liệu vào mảng tạm
        for (int i = 0; i < n1; ++i)
            L[i] = arr[l + i];
        for (int j = 0; j < n2; ++j)
            R[j] = arr[m + 1 + j];

        // Merge các mảng tạm lại

        // Chỉ mục ban đầu của 2 mảng con
        int i = 0, j = 0;

        // Chỉ mục ban đầu của mảng phụ được hợp nhất
        int k = l;
        while (i < n1 && j < n2) {
            if (L[i] <= R[j]) {
                arr[k] = L[i];
                i++;
            } else {
                arr[k] = R[j];
                j++;
            }
            k++;
        }

        // Sao chép các phần tử còn lại của L[] nếu có
        while (i < n1) {
            arr[k] = L[i];
            i++;
            k++;
        }

        // Sao chép các phần tử còn lại của R[] nếu có
        while (j < n2) {
            arr[k] = R[j];
            j++;
            k++;
        }
    }

    void sort(int arr[], int l, int r) {
        if (l < r) {

            // Tìm điểm chính giữa
            int m = (l + r) / 2;

            // Hàm đệ quy tiếp tục chia đôi
            sort(arr, l, m);
            sort(arr, m + 1, r);

            merge(arr, l, m, r);
        }
    }

    // In các phần tử của mảng
    static void printArray(int arr[]) {
        int n = arr.length;
        for (int i = 0; i < n; ++i)
            System.out.print(arr[i] + " ");
        System.out.println();
    }

    public static void main(String args[]) {
        int arr[] = {38, 27, 43, 3, 9, 82, 10};

        System.out.println("Mảng ban đầu:");
        printArray(arr);

        MergeSort ob = new MergeSort();
        ob.sort(arr, 0, arr.length - 1);

        System.out.println("Mảng sau khi sắp xếp:");
        printArray(arr);
    }
}

Merge Sort là một trong những thuật toán sắp xếp nhanh được sử dụng rộng rãi. Giả sử có một máy tính giải được $10^9$ bài toán trong 1 giây. Trong trường hợp đó, để sắp xếp một dãy số gồm $10^6$ số thì Merge Sort tốn chưa tới 1 giây còn Bubble Sort tốn tới 1000 giây.

Merge Sort còn có tốc độ ổn định. Vẫn là một máy tính giải được $10^9$ bài toán trong 1 giây. Trong khi đó nếu ta dùng Quick Sort sắp xếp 1 dãy chứa $10^6$ số thì vẫn có trường hợp ta phải chờ 1000 giây để sắp xếp xong, còn Merge Sort thì luôn luôn chưa tới 1 giây.

Merge Sort còn giữ được thứ tự của các phần tử bằng nhau sau khi sắp xếp. Chẳng hạn như khi ta cần sắp xếp một mảng gồm các điểm theo trong hệ tọa độ Oxy theo chiều tăng dần của hoành độ, nếu hoành độ bằng nhau thì sắp tăng dần theo tung độ. Trong trường hợp đó, ta chỉ cần dùng Merge Sort sắp xếp tung độ sau đó lại dùng Merge Sort sắp xếp hoành độ.

Merge sort là một giải thuật sắp xếp mà có thời gian thực hiện là O(NlogN) trong mọi trường hợp, bởi vậy mà với dữ liệu lớn và cần ít thao tác sắp xếp thì nó sẽ tối ưu hơn Quick sort. Nó chỉ có 1 nhược điểm đó là code hơi khó cài đặt.

Bài viết mang tính chất “ghi chú, lưu trữ, chia sẻ và phi lợi nhuận”.
Nếu bạn thấy hữu ích, đừng quên chia sẻ với bạn bè và đồng nghiệp của mình nhé!

Happy coding! 😎 👍🏻 🚀 🔥