Tree
1. Giới thiệu
Cấu trúc dữ liệu cây biểu diễn các nút (node) được kết nối bởi các cạnh. Chúng ta sẽ tìm hiểu về Cây nhị phân (Binary Tree) và Cây tìm kiếm nhị phân (Binary Search Tree) trong phần này.
Cây nhị phân là một cấu trúc dữ liệu đặc biệt được sử dụng cho mục đích lưu trữ dữ liệu. Một cây nhị phân có một điều kiện đặc biệt là mỗi nút có thể có tối đa hai nút con. Một cây nhị phân tận dụng lợi thế của hai kiểu cấu trúc dữ liệu: một mảng đã sắp thứ tự và một danh sách liên kết (Linked List), do đó việc tìm kiếm sẽ nhanh như trong mảng đã sắp thứ tự và các thao tác chèn và xóa cũng sẽ nhanh bằng trong Linked List.
2. Các khái niệm cơ bản về cây nhị phân
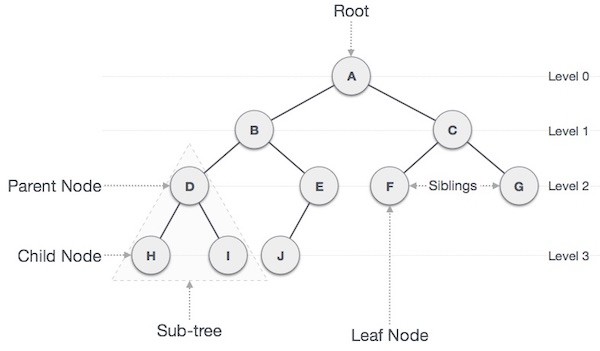
Dưới đây là một số khái niệm quan trọng liên quan tới cây nhị phân:
- Đường: là một dãy các nút cùng với các cạnh của một cây.
- Nút gốc (Root): nút trên cùng của cây được gọi là nút gốc. Một cây sẽ chỉ có một nút gốc và một đường xuất phát từ nút gốc tới bất kỳ nút nào khác. Nút gốc là nút duy nhất không có bất kỳ nút cha nào.
- Nút cha: bất kỳ nút nào ngoại trừ nút gốc mà có một cạnh hướng lên một nút khác thì được gọi là nút cha.
- Nút con: nút ở dưới một nút đã cho được kết nối bởi cạnh dưới của nó được gọi là nút con của nút đó.
- Nút lá: nút mà không có bất kỳ nút con nào thì được gọi là nút lá.
- Cây con: cây con biểu diễn các con của một nút.
- Truy cập: kiểm tra giá trị của một nút khi điều khiển là đang trên một nút đó.
- Duyệt: duyệt qua các nút theo một thứ tự nào đó.
- Bậc: bậc của một nút biểu diễn số con của một nút. Nếu nút gốc có bậc là 0, thì nút con tiếp theo sẽ có bậc là 1, và nút cháu của nó sẽ có bậc là 2, …
- Khóa (Key): biểu diễn một giá trị của một nút dựa trên những gì mà một thao tác tìm kiếm thực hiện trên nút.
Cây nhị phân có một số đặc tính thú vị:
- Tổng số nút trên mỗi “cấp độ” tăng gấp đôi khi bạn di chuyển xuống cây.
- Số nút ở cấp cuối cùng bằng tổng số nút ở tất cả các cấp khác, cộng với 1
Mỗi phần tử dữ liệu được lưu trữ trong cấu trúc cây được gọi là một nút. Nút Cây chứa các phần sau:
- Dữ liệu
- Con trỏ trái
- Con trỏ phải Trong Java, chúng ta có thể biểu diễn một nút của cây bằng cách sử dụng lớp. Dưới đây là một ví dụ về một nút của cây với dữ liệu số nguyên.
1
2
3
4
5
6
7
8
9
10
static class Node {
int value;
Node left, right;
Node(int value) {
this.value = value;
left = null;
right = null;
}
}
Bây giờ bạn đã biết cây nhị phân là gì, hãy cùng tìm hiểu các loại cây nhị phân khác nhau.
3. Các loại cây nhị phân
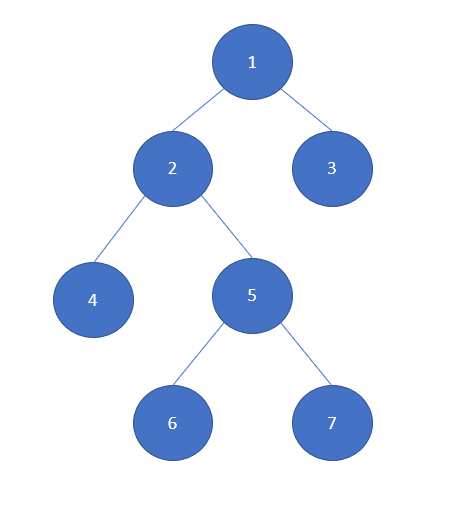
Cây nhị phân đầy đủ
Cây nhị phân đầy đủ là cây nhị phân trong đó mỗi nút có đúng 0 hoặc 2 nút con. Ví dụ
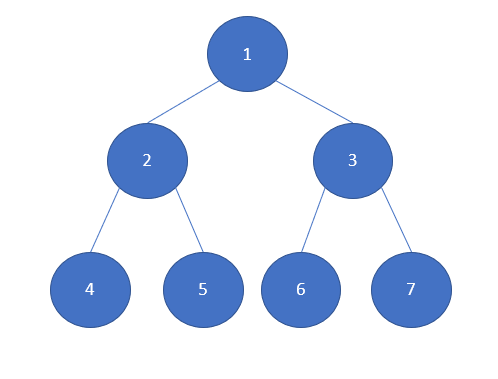
Cây nhị phân hoàn hảo
Cây nhị phân là Cây nhị phân hoàn hảo nếu tất cả các nút bên trong đều có hai nút con và có tất cả các lá ở cùng mức. Ví dụ về cây nhị phân hoàn hảo là:
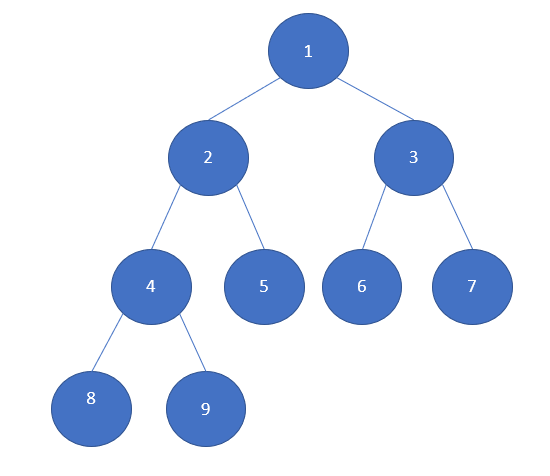
Cây nhị phân hoàn chỉnh
Cây nhị phân hoàn chỉnh là cây nhị phân trong đó mọi cấp, ngoại trừ cấp cuối cùng, được lấp đầy hoàn toàn và tất cả các nút ưu tiên dồn về bên trái. Một ví dụ về cây nhị phân hoàn chỉnh là:
Bây giờ bạn đã biết về các loại cây nhị phân khác nhau, hãy cùng tìm hiểu cách tạo cây nhị phân.
4. Triển khai cây nhị phân
Đối với việc triển khai, có một lớp Node bổ trợ sẽ lưu trữ các giá trị int và giữ một tham chiếu đến từng nút con. Bước đầu tiên là tìm vị trí mà chúng ta muốn thêm một nút mới để giữ cho cây được sắp xếp. Chúng ta sẽ phải tuân theo các quy tắc này bắt đầu từ nút gốc:
- nếu giá trị của nút mới thấp hơn giá trị của nút hiện tại, chuyển đến nút con bên trái
- nếu giá trị của nút mới lớn hơn giá trị của nút hiện tại, chuyển đến nút con bên phải
- khi nút hiện tại rỗng, chúng tôi đã đạt đến nút lá, chèn nút mới vào vị trí đó Bây giờ, hãy xem cách chúng ta có thể triển khai logic này thông qua ví dụ sau đây:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
public class TreeDemo {
static class Node {
int value;
Node left, right;
Node(int value) {
this.value = value;
left = null;
right = null;
}
}
public void insert(Node node, int value) {
if (value < node.value) {
if (node.left != null) {
insert(node.left, value);
} else {
System.out.println(" Chèn " + value + " vào bên trái của " + node.value);
node.left = new Node(value);
}
} else if (value > node.value) {
if (node.right != null) {
insert(node.right, value);
} else {
System.out.println(" Chèn " + value + " vào bên phải của " + node.value);
node.right = new Node(value);
}
}
}
public void traverseInOrder(Node node) {
if (node != null) {
traverseInOrder(node.left);
System.out.print(" " + node.value);
traverseInOrder(node.right);
}
}
public static void main(String args[]) {
TreeDemo tree = new TreeDemo();
Node root = new Node(5);
System.out.println("Ví dụ cây nhị phân");
System.out.println("Xây dựng cây nhị phần với nút gốc là: " + root.value);
tree.insert(root, 2);
tree.insert(root, 4);
tree.insert(root, 8);
tree.insert(root, 6);
tree.insert(root, 7);
tree.insert(root, 3);
tree.insert(root, 9);
System.out.println("Duyệt cây theo thứ tự:");
tree.traverseInOrder(root);
}
}
Trong ví dụ trên, chúng ta đã sử dụng tính năng duyệt theo thứ tự. Việc duyệt theo thứ tự bao gồm việc truy cập đầu tiên vào cây con bên trái, sau đó đến nút gốc và cuối cùng là cây con bên phải. Có nhiều cách khác để duyệt cây. Bạn hãy kiểm tra chúng.
5. Một số phương pháp duyệt cây
Duyệt theo chiều sâu
Duyệt cây theo chiều sâu là một loại tìm kiếm mà bạn đi sâu nhất có thể xuống theo một đường duyệt trước khi sao lưu và thử với một đường duyệt khác. Có một số cách để thực hiện tìm kiếm theo chiều sâu: Theo thứ tự: (code bên trên)
Theo kiểu Pre-Order: truy cập vào nút gốc trước tiên, sau đó đến cây con bên trái và cuối cùng là cây con bên phải.
(chỉ việc thay hàm
traverseInOrder()trên code mẫu thànhtraversePreOrder())
1
2
3
4
5
6
7
public void traversePreOrder(Node node) {
if (node != null) {
System.out.print(" " + node.value);
traversePreOrder(node.left);
traversePreOrder(node.right);
}
}
Theo kiểu Post-Order: truy cập vào cây con bên trái trước tiên, sau đó đến cây con bên phải và nút gốc ở cuối cùng.
(chỉ việc thay hàm traverseInOrder() trên code mẫu thành traversePreOrder())
1
2
3
4
5
6
7
public void traversePostOrder(Node node) {
if (node != null) {
traversePostOrder(node.left);
traversePostOrder(node.right);
System.out.print(" " + node.value);
}
}
Duyệt theo chiều rộng
Phương pháp duyệt này truy cập tất cả các nút của một cấp trước khi chuyển sang cấp tiếp theo. Nó giống như ném một hòn đá vào giữa ao. Các nút bạn khám phá “gợn sóng” từ điểm bắt đầu. Duyệt theo chiều rộng còn được gọi là thứ tự cấp và truy cập tất cả các cấp của cây bắt đầu từ gốc và từ trái sang phải.
Cây nhị phân là loại cấu trúc dữ liệu được sử dụng nhiều trong hầu hết tất cả các lĩnh vực của đời sống. Nó càng đặc biệt lợi hại khi kết hợp với một số thuật toán khác – điều ưa chuộng và bắt buộc với mỗi lập trình viên lành nghề. Nhưng ở bước khởi đầu, Hãy đảm bảo rằng bạn luyện tập nhiều nhất có thể và hoàn thành tốt trải nghiệm của mình.
Bài viết mang tính chất “ghi chú, lưu trữ, chia sẻ và phi lợi nhuận”.
Nếu bạn thấy hữu ích, đừng quên chia sẻ với bạn bè và đồng nghiệp của mình nhé!
Happy coding! 😎 👍🏻 🚀 🔥